Углы в пифагоровом треугольнике

В математике есть определенные каноны, которые явились, так сказать, фундаментом или основанием всего последующего развития современной математики. Одним из этих канонов, по праву можно считать теорему Пифагора.

Кому еще со школьных времен не известна смешная формулировка теоремы Пифагора: "Пифагоровы штаны во все стороны равны". Ну да, правильно это звучит так: "квадрат гипотенузы равен сумме квадратов катетов ", но про штаны гораздо лучше запоминается.

Нагляднее всего это видно на треугольнике со сторонами 3-4-5. Но если изучить внимательно использование такого треугольника в древней истории, то можно заметить одну занимательную вещь и называется она ни как по другому, как Египетский треугольник.

Этот самый философ и математик Пифагор Самосский из Греции, именем которого и названа эта теорема, жил примерно 2,5 тысяч лет тому назад. Ну конечно дошедшая до нашего времени биография Пифагора не совсем достоверна, но, тем не менее, известно что Пифагор много путешествовал по странам Востока. В том числе он был и Египте и Вавилоне. В Южной Италии Пифагор основал свою знаменитую "Пифагорову школу", которая сыграла очень даже важную роль, как в научной, так и политической жизни древней Греции. С тех времен по преданиям Плутарха, Прокла и других известных математиков того времени, считалось, что эта теорема до Пифагора известна не была и именно по этому её назвали его именем.

Но история говорит что это не так. Обратимся туда, где бывал Пифагор и что видел, прежде чем сформулировать свою теорему. Африка, Египет. Бесконечный и однообразный океан песка, почти ни какой растительности. Редкие кустики растений, едва заметные верблюжьи следы. Раскаленная пустыня. Солнце и то кажется тусклым, как будто покрытым этим вездесущим мелким песком.

И вдруг, как мираж, как видение, на горизонте возникают строгие очертания пирамид, изумительных по своим идеальным геометрическим формам, устремленным к палящему солнцу. Своими огромными размерами, и совершенством своих форм они изумляют.

Скорее всего, Пифагор их видел в ином виде, нежели как они выглядят сейчас. Это были сияющие полированные громады с четкими гранями на фоне многоколонных прилегающих храмов. Рядом с величественными царскими пирамидами стояли пирамиды поменьше: жен и родичей фараонов.

Власть фараонов Древнего Египта была непререкаемой. Фараонов считали божеством и отдавали им божественные почести. Фараон-бог был вершителем судьбы народа и его покровителем. Даже после смерти культ фараона имел преогромное значение. Умершего фараона сохраняли веками, и для сохранения тела фараона сооружали гигантские пирамиды. Величие, архитектура и размеры этих пирамид поражают и сейчас. Недаром эти сооружения относили к одному из семи чудес света.

Изначально назначение пирамид было не только как усыпальниц фараонов. Считают что они сооружались как атрибуты могущества, величия, и богатства Египта. Это памятники культуры того времени, хранилища истории страны и сведений о жизни фараона и его народа, собрание предметов быта того времени. Кроме того однозначно, что пирамиды имели определенное "научное содержание". Их ориентирование на местности, их форма, размеры и каждая деталь, каждый элемент настолько тщательно продумывались, что должны были продемонстрировать высокий уровень знаний создателей пирамид. Очевидно что они строились на тысячелетия, "навечно". И недаром арабская пословица гласит: "Все на свете страшится времени, а время страшится пирамид".

Своим аналитическим умом Пифагор не мог не заметить определенную закономерность в формах и геометрических размерах пирамид. Скорее всего, это и натолкнуло Пифагора на анализ этих размеров, что впоследствии и было им выражено своей знаменитой теоремой, от которой ныне и отталкивается современная геометия.

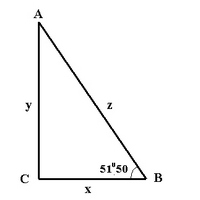
Среди множества пирамид сохранившихся до нашего времени особое место занимает пирамида Хеопса. Если рассмотреть геометрическую модель этой пирамиды и восстановить её первоначальную форму, то очевидно, что её поперечное сечение представляет собой два треугольника с внутренним углом равным 51°50′.

Сейчас пирамида является усеченной, но это разрушения времени, а если геометрически восстановить её в первоначальном виде, то получается что стороны этих треугольников равны: основание СВ = 116, 58 м, высота АС = 148,28 м.

Отношение катетов у/х = 148,28/116,58 = 1,272. А это величина тангеса угла 51град 50 мин. Получается, что в основу треугольника АСВ пирамиды Хеопса было заложено отношение AC/CB = 1,272. Такой прямоугольный треугольник называется "золотым" прямоугольным треугольником.

Получается что основной "геометрической идеей" пирамиды Хеопса является "золотой" прямоугольный треугольник. Но особой в этом отношении является пирамида Хефрена. Угол наклона боковых граней у этой пирамиды равен 53°12, при котором отношение катетов прямоугольного треугольника 4:3. Такой треугольник называют "священным" или "египетским" треугольником. По мнению многих известных историков, "египетскому" треугольнику в древности придавали особый магический смысл. Так Плутарх писал, что египтяне сопоставляли природу Вселенной со "священным" треугольником: символически они уподобляли вертикальный катет мужу, основание – жене, а гипотенузу – тому, что рождается от обоих.

Для египетского треугольника со сторонами 3:4:5 справедливо равенство: 32 + 42 = 52, а это и есть знаменитая теорема Пифагора. По неволе напрашивается вопрос: не это ли соотношение хотели увековечить египетские жрецы, построив пирамиду в основе которой лежит треугольник 3:4:5. Пирамида Хефрена наглядное подтверждение того что знаменитая теорема была известна египтянам задолго до ее открытия Пифагором.

Неизвестно как это попало к древним египтянам, то ли это заслуга их ученых, то ли это дар из вне, не исключается и то, что это дар внеземной цивилизации, но использование такого треугольника давало египетским строителям очень существенную и к тому же простую возможность при возведении таких огромных сооружений соблюдать точные геометрические размеры. Ведь свойства этого треугольника таковы, что его угол между катетами является равный 90 градусов. То есть использование такого элемента позволяет обеспечить точную перпендикулярность сопрягаемых элементов и естественно всей конструкции, что и подтверждает архитектура древнего Египта.

Получить прямой угол без необходимых инструментов не просто. Но если воспользоваться этим треугольником, оказывается все достаточно просто. Нужно взять обычную веревку, разделить её на 12 равных частей, и из них сложить треугольник, стороны которого будут равны 3, 4 и 5 частям. Угол между сторонами длиной 3 и 4 части оказывается и есть прямой. Вот это и есть Египетский треугольник Пифагора.

Во многих исторических письменах имеются следы, что уникальные свойства "египетского треугольника" были известны и широко использовались за много веков до Пифагора и не только в Египте, но и далеко за его пределами: в Месопотамии, в древнем Китае, в Вавилоне.

Знаменитая древнеегипетская пословица "Делай, как делается", дошедшая до наших дней, наталкивает на мысль что сами египтяне, возводившие эти строительные шедевры, были простыми исполнителями и особыми знаниями не обладали, а все секреты были скрыты от непосвященных. Ведь работами на строительстве руководили жрецы – члены особой привилегированной замкнутой касты. Они были хранителями древних знаний, которые держались в секрете. Но пытливый ум великого мыслителя Пифагора сумел разгадать один их этих секретов.

Умы людей всегда будоражат разнообразные загадки, и это, вероятно, будет всегда. Египетский треугольник, хоть и известен человечеству с незапамятных времён, все-таки одна из не полностью разгаданных тайн.

Ведь, что не говори, а форма египетского треугольника и проста, и в то же время гармонична, по своему он даже красив. И с ним достаточно легко работать. Для этого можно использовать самые простые инструменты – линейку и циркуль. Использую этот незатейливый элемент и его симметричные отображения, можно получить красивые, гармоничные фигуры. Это и мальтийский крест, и серединное сечение пирамиды Хефрена, и фрактальный ряд убывающих – возрастающих, по размерам египетских треугольников в соответствии с правилом золотого сечения. Это удивительное богатство гармоничных пропорций.

До сих пор в мире есть много пытливые люди, которые как безумцы изобретают вечный двигатель, ищут квадратуру круга, философский камень и книгу мёртвых. Скорее всего, усилия их тщетны, но даже в случае с Египетским треугольником, ясно что "простых тайн" на земле еще много.

1.Теорема Пифагора

Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Доказательство.

1. Разделим каждую сторону большого квадрата на два отрезка x и y точкой. И проведем через эти точки отрезки.

2. Тогда треугольники 1,2,3,4 равны по двум сторонам и углу между ними.

3. Т.к. сумма углов α + β = 90°, то фигура внутри большого квадрата тоже квадрат. (Все стороны = с и все углы = 90° )

4. Площадь большого квадрата равна сумме площадей малого квадрата и 4-х треугольников. (Рис.1)

Рис.1 Теорема Пифагора.

2.Египетский треугольник

Пусть дан треугольник со сторонами АВ = a, ВС = b, АС = c. При условии, что а 2 + b 2 = с 2 . Доказать, что угол, лежащий против стороны с, прямой.

Допустим, что треугольник АВС не прямоугольный. Тогда можно опустить высоту на сторону АС – h (Рис.2). Из двух прямоугольных треугольников ABD и DBC составим следующую систему уравнений по теореме Пифагора. Обозначим AD как х, BD – высота h.

Но по условию задачи а 2 + b 2 = с 2 . Следовательно х = 0 и сторона а = h. Т.е. угол между сторонами АВ и АС – прямой.

В древнем Египте данное соотношение применялось очень широко. Например для построения прямого угла между сторонами при строительстве зданий и сооружений. Или при измерении прямых углов пахотных земель. Так как зная соотношение, можно легко построить прямой угол. По этой причине треугольник со сторонами 3,4,5 ед. называют Египетским треугольником.

Рис.2 Египетский треугольник.

3.Соотношение между углами и сторонами в прямоугольном треугольнике

Пусть дан прямоугольный треугольник АВС. Проведем прямую ЕF параллельную стороне АВ (Рис.3). Тогда по теореме о пропорциональных отрезках:

Т.е. соs α не зависит от размеров прямоугольного треугольника, а зависит только от величины угла. Тогда по теореме Пифагора sin α также зависит только от величины угла. А следовательно tg α и ctg α.

Отсюда можно сделать следующие выводы:

AB = BC sin α
AC = BC cos α
AB = AC tg α
AC = AB ctg α

Рис.3 Соотношение между углами и сторонами в прямоугольном треугольнике.

4.Основные тригонометрические тождества

Пусть дан прямоугольный треугольник со сторонами a,b,c. (Рис.4)

Рис.4 Основные тригонометрические тождества.

5.Пример 1

У треугольника одна сторона равна 1 м, а прилегающие к ней углы 30° и 45°. Найдите другие стороны треугольника. (рис.5)

Так как один из углов 30 градусов, то катет, лежащий против этого угла равен половине гипотенузы, т.е. h = b/2. А следовательно КС = h, т.к. угол β = 45 градусов.

Рис.5 Задача. У треугольника одна сторона равна 1 м.

Пример 2

Найдите высоту равнобокой трапеции, если ее основания равны 6 м и 12 м, а боковая сторона равна 5 м. (Рис.6)

Решение:

Пусть ABCD данная трапеция. ВЕ перпендикуляр, опущенный на основание AD. Тогда АЕ = (12 – 6)/ 2 = 3 м. Так как АЕ = FD.

По теореме Пифагора:

АВ 2 = AE 2 + BE 2

Рис.6 Задача. Найдите высоту равнобокой трапеции.

Пример 3

Докажите, что расстояние между двумя точками на сторонах треугольника не больше большей из его сторон. (Рис.7)

Доказательство:

Пусть ABC данный треугольник. АС – его большая сторона. Проведем отрезок DE параллельно стороне АС. Необходимо доказать, что отрезок DE меньше стороны АС. Если мы докажем, что отрезок DE меньше большей стороны АС, то при взятии двух других точек треугольника на других его меньших сторонах, отрезок между этими точками будет также меньше стороны АС.

Опустим перпендикуляр BF на большую сторону АС. Составим следующее соотношение:

АС = АВ сos α + ВС cos β

Тогда отрезок DE будет равен:

DE = DB сos α + ВE cos β

Так как DB Рис.7 Задача. Докажите, что расстояние между двумя точками.

Пример 4

Докажите, что прямая, отстоящая от центра окружности на расстояние меньше радиуса, пересекает окружность в двух точках. (Рис.8)

Доказательство:

Пусть дана окружность с центром в точке О. И прямая а, отстоящая от центра окружности точки О, на расстояние ОЕ = h h, то прямая а будет иметь две точки пересечения. Так как

h = ОА*cos α = ОВ*cos (-α)

Радиусы ОА и ОВ можно рассматривать как две наклонные, отложенные в двух полуплоскостях, в треугольнике АОВ перпендикуляра ОЕ.

Рис.8 Задача. Докажите, что прямая, отстоящая от центра окружности.

Пример 5

Даны три положительных числа a,b,c. Докажите, что если каждое из этих чисел меньше суммы двух других, то существует треугольник со сторонами a,b,c. (Рис.9)

Доказательство:

Пусть даны три точки. Если эти три точки лежат на одной прямой, например А,Е,С, то расстояния между этими точками связаны соотношением: АС = АЕ + ЕС

Отсюда видно, что каждое из трех расстояний не больше двух других. Т.е. расстояние между точками А и С не больше двух расстояний АЕ и ЕС.

Если взять три точки, не лежащих на одной прямой, например А,В,С и опустить перпендикуляр ВЕ, то АС AB + BC (Рис.9 б). Тогда концы отрезков АВ и СВ не смогут совпасть в точке В. Так как, если даже отрезки такой же длины отложить на отрезке АС, то получится, что

Таким образом, если числа a,b и с принять за длины отрезков, то концы отрезков АВ и СВ не смогут совпасть в одной точке В. Между ними образуется некое расстояние ВВ₁ и построить треугольник не получится.

Рис.9 Задача. Даны три положительных числа.

Отрывок из книги математика Иэна Стюарта о доказательствах теоремы Пифагора, правильных геометрических фигурах и формуле для решения уравнений 5-й степени

Пифагорова гипотенуза

Пифагоровы треугольники имеют прямой угол и целочисленные стороны. У простейшего из них самая длинная сторона имеет длину 5, остальные — 3 и 4. Всего существует 5 правильных многогранников. Уравнение пятой степени невозможно решить при помощи корней пятой степени — или любых других корней. Решетки на плоскости и в трехмерном пространстве не имеют пятилепестковой симметрии вращения, поэтому такие симметрии отсутствуют и в кристаллах. Однако они могут быть у решеток в четырехмерном пространстве и в занятных структурах, известных как квазикристаллы.

Гипотенуза самой маленькой пифагоровой тройки

Теорема Пифагора гласит, что самая длинная сторона прямоугольного треугольника (пресловутая гипотенуза) соотносится с двумя другими сторонами этого треугольника очень просто и красиво: квадрат гипотенузы равен сумме квадратов двух других сторон.

Традиционно мы называем эту теорему именем Пифагора, но на самом деле история ее достаточно туманна. Глиняные таблички позволяют предположить, что древние вавилоняне знали теорему Пифагора задолго до самого Пифагора; славу первооткрывателя принес ему математический культ пифагорейцев, сторонники которого верили, что Вселенная основана на числовых закономерностях. Древние авторы приписывали пифагорейцам — а значит, и Пифагору — самые разные математические теоремы, но на самом деле мы представления не имеем о том, какой математикой занимался сам Пифагор. Мы даже не знаем, могли ли пифагорейцы доказать теорему Пифагора или просто верили в то, что она верна. Или, что наиболее вероятно, у них были убедительные данные о ее истинности, которых тем не менее не хватило бы на то, что мы считаем доказательством сегодня.

Доказательства Пифагора

Первое известное доказательство теоремы Пифагора мы находим в «Началах» Евклида. Это достаточно сложное доказательство с использованием чертежа, в котором викторианские школьники сразу узнали бы «пифагоровы штаны»; чертеж и правда напоминает сохнущие на веревке подштанники. Известны буквально сотни других доказательств, большинство из которых делает доказываемое утверждение более очевидным.

Одно из простейших доказательств — это своего рода математический пазл. Возьмите любой прямоугольный треугольник, сделайте четыре его копии и соберите их внутри квадрата. При одной укладке мы видим квадрат на гипотенузе; при другой — квадраты на двух других сторонах треугольника. При этом ясно, что площади в том и другом случае равны.

Рассечение Перигаля — еще одно доказательство-пазл.

Существует также доказательство теоремы с использованием укладки квадратов на плоскости. Возможно, именно так пифагорейцы или их неизвестные предшественники открыли эту теорему. Если взглянуть на то, как косой квадрат перекрывает два других квадрата, то можно увидеть, как разрезать большой квадрат на куски, а затем сложить из них два меньших квадрата. Можно увидеть также прямоугольные треугольники, стороны которых дают размеры трех задействованных квадратов.

Есть интересные доказательства с использованием подобных треугольников в тригонометрии. Известно по крайней мере пятьдесят различных доказательств.

Пифагоровы тройки

В теории чисел теорема Пифагора стала источником плодотворной идеи: найти целочисленные решения алгебраических уравнений. Пифагорова тройка — это набор целых чисел a, b и c, таких что

Геометрически такая тройка определяет прямоугольный треугольник с целочисленными сторонами.

Самая маленькая гипотенуза пифагоровой тройки равна 5.

Другие две стороны этого треугольника равны 3 и 4. Здесь

32 + 42 = 9 + 16 = 25 = 52.

Следующая по величине гипотенуза равна 10, потому что

62 + 82 = 36 + 64 = 100 = 102.

Однако это, по существу, тот же треугольник с удвоенными сторонами. Следующая по величине и по-настоящему другая гипотенуза равна 13, для нее

52 + 122 = 25 + 144 = 169 = 132.

Евклид знал, что существует бесконечное число различных вариантов пифагоровых троек, и дал то, что можно назвать формулой для нахождения их всех. Позже Диофант Александрийский предложил простой рецепт, в основном совпадающий с евклидовым.

Возьмите любые два натуральных числа и вычислите:

их удвоенное произведение;

разность их квадратов;

сумму их квадратов.

Три получившихся числа будут сторонами пифагорова треугольника.

Возьмем, к примеру, числа 2 и 1. Вычислим:

удвоенное произведение: 2 × 2 × 1 = 4;

разность квадратов: 22 — 12 = 3;

сумма квадратов: 22 + 12 = 5,

и мы получили знаменитый треугольник 3–4–5. Если взять вместо этого числа 3 и 2, получим:

удвоенное произведение: 2 × 3 × 2 = 12;

разность квадратов: 32 — 22 = 5;

сумму квадратов: 32 + 22 = 13,

и получаем следующий по известности треугольник 5 — 12 — 13. Попробуем взять числа 42 и 23 и получим:

удвоенное произведение: 2 × 42 × 23 = 1932;

разность квадратов: 422 — 232 = 1235;

сумма квадратов: 422 + 232 = 2293,

никто никогда не слышал о треугольнике 1235–1932–2293.

Но эти числа тоже работают:

12352 + 19322 = 1525225 + 3732624 = 5257849 = 22932.

В диофантовом правиле есть еще одна особенность, на которую уже намекали: получив три числа, мы можем взять еще одно произвольное число и все их на него умножить. Таким образом треугольник 3–4–5 можно превратить в треугольник 6–8–10, умножив все стороны на 2, или в треугольник 15–20–25, умножив все на 5.

Если перейти на язык алгебры, правило приобретает следующий вид: пусть u, v и k — натуральные числа. Тогда прямоугольный треугольник со сторонами

2kuv и k (u2 — v2) имеет гипотенузу

Существуют и другие способы изложения основной идеи, но все они сводятся к описанному выше. Этот метод позволяет получить все пифагоровы тройки.

Правильные многогранники

Существует ровным счетом пять правильных многогранников. Правильный многогранник (или полиэдр) — это объемная фигура с конечным числом плоских граней. Грани сходятся друг с другом на линиях, именуемых ребрами; ребра встречаются в точках, именуемых вершинами.

Кульминацией евклидовых «Начал» является доказательство того, что может быть только пять правильных многогранников, то есть многогранников, у которых каждая грань представляет собой правильный многоугольник (равные стороны, равные углы), все грани идентичны и все вершины окружены равным числом одинаково расположенных граней. Вот пять правильных многогранников:

тетраэдр с четырьмя треугольными гранями, четырьмя вершинами и шестью ребрами;

куб, или гексаэдр, с 6 квадратными гранями, 8 вершинами и 12 ребрами;

октаэдр с 8 треугольными гранями, 6 вершинами и 12 ребрами;

додекаэдр с 12 пятиугольными гранями, 20 вершинами и 30 ребрами;

икосаэдр с 20 треугольными гранями, 12 вершинами и 30 ребрами.

Правильные многогранники можно найти и в природе. В 1904 г. Эрнст Геккель опубликовал рисунки крохотных организмов, известных как радиолярии; многие из них по форме напоминают те самые пять правильных многогранников. Возможно, правда, он немного подправил природу, и рисунки не отражают полностью форму конкретных живых существ. Первые три структуры наблюдаются также в кристаллах. Додекаэдра и икосаэдра в кристаллах вы не найдете, хотя неправильные додекаэдры и икосаэдры там иногда попадаются. Настоящие додекаэдры могут возникать в виде квазикристаллов, которые во всем похожи на кристаллы, за исключением того, что их атомы не образуют периодической решетки.

Бывает интересно делать модели правильных многогранников из бумаги, вырезав предварительно набор соединенных между собой граней — это называется разверткой многогранника; развертку складывают по ребрам и склеивают соответствующие ребра между собой. Полезно добавить к одному из ребер каждой такой пары дополнительную площадку для клея, как показано на рис. 39. Если такой площадки нет, можно использовать липкую ленту.

Уравнение пятой степени

Не существует алгебраической формулы для решения уравнений 5-й степени.

В общем виде уравнение пятой степени выглядит так:

ax5 + bx4 + cx3 + dx2 + ex + f = 0.

Проблема в том, чтобы найти формулу для решений такого уравнения (у него может быть до пяти решений). Опыт обращения с квадратными и кубическими уравнениями, а также с уравнениями четвертой степени позволяет предположить, что такая формула должна существовать и для уравнений пятой степени, причем в ней, по идее, должны фигурировать корни пятой, третьей и второй степени. Опять же, можно смело предположить, что такая формула, если она существует, окажется очень и очень сложной.

Это предположение в конечном итоге оказалось ошибочным. В самом деле, никакой такой формулы не существует; по крайней мере не существует формулы, состоящей из коэффициентов a, b, c, d, e и f, составленной с использованием сложения, вычитания, умножения и деления, а также извлечения корней. Таким образом, в числе 5 есть что-то совершенно особенное. Причины такого необычного поведения пятерки весьма глубоки, и потребовалось немало времени, чтобы в них разобраться.

Первым признаком проблемы стало то, что, как бы математики ни старались отыскать такую формулу, какими бы умными они ни были, они неизменно терпели неудачу. Некоторое время все считали, что причины кроются в неимоверной сложности формулы. Считалось, что никто просто не может как следует разобраться в этой алгебре. Однако со временем некоторые математики начали сомневаться в том, что такая формула вообще существует, а в 1823 г. Нильс Хендрик Абель сумел доказать обратное. Такой формулы не существует. Вскоре после этого Эварист Галуа нашел способ определить, решаемо ли уравнение той или иной степени — 5-й, 6-й, 7-й, вообще любой — с использованием такого рода формулы.

Вывод из всего этого прост: число 5 особенное. Можно решать алгебраические уравнения (при помощи корней n-й степени для различных значений n) для степеней 1, 2, 3 и 4, но не для 5-й степени. Здесь очевидная закономерность заканчивается.

Никого не удивляет, что уравнения степеней больше 5 ведут себя еще хуже; в частности, с ними связана такая же трудность: нет общих формул для их решения. Это не означает, что уравнения не имеют решений; это не означает также, что невозможно найти очень точные численные значения этих решений. Все дело в ограниченности традиционных инструментов алгебры. Это напоминает невозможность трисекции угла при помощи линейки и циркуля. Ответ существует, но перечисленные методы недостаточны и не позволяют определить, каков он.

Кристаллографическое ограничение

Кристаллы в двух и трех измерениях не имеют 5-лучевой симметрии вращения.

Атомы в кристалле образуют решетку, то есть структуру, которая периодически повторяется в нескольких независимых направлениях. К примеру, рисунок на обоях повторяется по длине рулона; кроме того, он обычно повторяется и в горизонтальном направлении, иногда со сдвигом от одного куска обоев к следующему. По существу, обои — это двумерный кристалл.

Существует 17 разновидностей обойных рисунков на плоскости (см. главу 17). Они различаются по типам симметрии, то есть по способам сдвинуть жестко рисунок таким образом, чтобы он точно лег сам на себя в первоначальном положении. К типам симметрии относятся, в частности, различные варианты симметрии вращения, где рисунок следует повернуть на определенный угол вокруг определенной точки — центра симметрии.

Порядок симметрии вращения — это то, сколько раз можно повернуть тело до полного круга так, чтобы все детали рисунка вернулись на первоначальные позиции. К примеру, поворот на 90° — это симметрия вращения 4-го порядка*. Список возможных типов симметрии вращения в кристаллической решетке вновь указывает на необычность числа 5: его там нет. Существуют варианты с симметрией вращения 2, 3, 4 и 6-го порядков, но ни один обойный рисунок не имеет симметрии вращения 5-го порядка. Симметрии вращения порядка больше 6 в кристаллах тоже не бывает, но первое нарушение последовательности происходит все же на числе 5.

Главная > Учебные материалы > Математика: Планиметрия. Страница 5
1 2 3 4 5 6 7 8 9 10 11 12